IASLonline NetArt: Theory

Thomas Dreher

History of Computer Art

II. Cybernetics
II.1 Basics of Cybernetics

auf Deutsch

• II.1.1 Ballistics
• II.1.2 Stochastics
• II.1.3 Information
• II.1.4 Feedback
• II.1.5 Homeostasis
• Illustrations Part I: Cybernetics: PPT / PDF
• Table of Contents
• Bibliography
• Previous Chapter
• Next Chapter

The basics of cybernetics were presented by technically constructed models (see chap. II.2). These models became fundamental for the development of cybernetic sculptures (see chap. II.3), meanwhile the information aesthetics based on cybernetics offered criteria for the artists programming computer graphics (see chap. III.2). This shows: There is no alternative to an introduction to cybernetics.

In 1948/49 Norbert Wiener and Claude Elwood Shannon published in their classic books on cybernetics and information theory the basics of the American army´s ballistic research in the Second World War. The calculation of the flight path of an enemy´s airplane presupposed to know how pilots navigate to reach their target. 1 However, in practice, the pilots changed their approach to targets according to their knowledge of the air defense and made forecasts of the meeting between an airplane and a projectile impossible. 2 The problem to predict this crash made relevant the problem to calculate the probability which flight path will be chosen (see chap. II.1.2).

The cybernetics´ basic texts are the fruits of the research for air defense 3 being able to resolve the feedback (see chap II.1.4) between the movements of the targets and the projectile much later with the development of missiles.

At first the integration of mathematics into engineering was discussed controversal by researchers of ballistics and cryptography. 4 "It was only in 1945, when the usefulness of mathematics was upgraded for strategic and technic tasks." 5 Before 1945 Wiener and Shannon investigated the fields of convergences between mathematics and engineering, and in their later published writings they laid down the basics for an understanding of the term information as integrating the opposing research poles (see chap. II.1.3). For mainframe computers the American and British army developed simultaneously uses in ballistics, early warning systems, and cryptography. 6

Left: Norbert Wiener (Cover of "Cybernetics", second edition, 1962).
Right: Claude Elwood Shannon with "Theseus" (1952) and the mouse navigating itself through the labyrinth (compare chap. II.2.2).
(Credit: MIT Museum, Boston / Nixdorf MuseumsForum, Paderborn)

Stochastics combine calculations of probabilities and statistics of frequencies. The possibilities of a system to combine its elements with each other can be restricted to probabilities by statistics informing about the frequency of their earlier occurrences. Predictions indicate the probability of a systems´ elements by indicating how often they appeared in the past and how these occurrences relate to all possible combinations : The reappearance of a more frequent used element is more probable than the reappearance of a seldom used element. Shannon used stochastics as a means to construct the English language for a second time by generating combinations of its elements and their combinations – following the frequencies of their occurrences. The computer calculates the possibilities of combinations fast and the frequency statistic of letters in units of a selected language serves to restrict these possibilities. In the course of this selection procedure the probability rises that the calculated possibilities and the chosen language coincide (see chap. III.1.3).

The approximation to a language by the recombination of its elements in regard to the frequencies´ statistics of their occurrences in the everyday language recalls procedures of the cryptography: The signs appearing often in a code are compared with the frequencies of signs in the language of the message to be decoded. Shannon won the characteristics of a not decryptable code with cryptographic methods: It should be constructed only by chance operations, it should be as extensive as the urtext, and it has to be kept secret. 7

For Shannon and Wiener the term information serves to denote a measure of a technical system´s capacity. A system´s technology can be able to transfer a certain amount of information. There is a distinction to be made between this measurement of its transmission capacity and the "semantic information" (see chap. III.1.3). 8 The basis of a definition of "information" is formed by the probable distribution of physical elements in a closed system with its tendency to entropy ("particular disorder, mixture"), as elaborated by Ludwig Boltzmann in his statistical thermodynamics 9, and its opposite, the "segregation" and "demixing" 10: information as negentropy. Cybernetics use the negation of entropy (negentropy) to develop a theory of information.

The alternative between two values is measured as 1 "bit". The relais of calculating machines and computers switch between the two values "0" and "1". 11 The possibilities to select are calculated as 2ⁿ. "n" stands for a number of decisions to choose one of the values "0" and "1". "Probabilities of selection" p₁, p₂...p_n belong to any independent, selectable sign. The probability of selection specifies the probability of an element´s occurrence (see chap. II.1.2). The probability of selection is multiplied by the logarithm with the base 2 of the probability of selection (p_nlog₂p_n). The products calculated with each probability of selection are added. The sum is negated to obtain the negentropy resp. the information "I":

I = - (p₁log₂p₁ + p₂log₂p₂ + ...p_nlog₂p_n)

I = - Σ p_nlog₂p_n (Σ = sum for n = 1 until n) 12

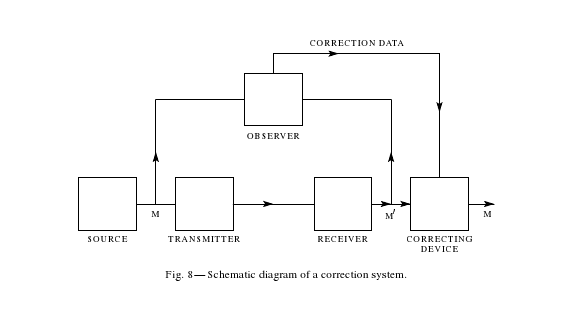
The system-internal transmission, its disturbances ("noise") and the feedback of the output into the system belong to the processing of input: The system controls the output by detecting the deviations and by reacting to them. This control procedure is called "feedback" 13 and the correcting technical element is named "observer". The "observer" couples the output to a circuit integrating the output data and correcting the subsequent output. In the case of deviations above a certain threshold this corrective "observer" is activated. 14

The connection between a system with an internal "observer" and its environment is recognized by an "external observer" 15 integrated by second- order cybernetics as part of a more extensive system. This more extensive system contains the environment of the first system as well as its observer orienting himself by perceptions and moving himself in this environment. 16 The external observer of the first system becomes an internal observer of the more extensive system.

Shannon, Claude Elwood: A Mathematical Theory of Communication. In: Bell System Technical Journal, Vol. 27/Nr.3, 1948, p. 409.

A system communicates with its environment by trying to use the internal structures for accomodations to disturbances being caused externally. William Ross Ashby´s cybernetic model of a "homeostasis" (see chap. II.2.1) presents a system with internal functions seeking equlibrium. 17 A multipartite system uses its internal variability to react to external disturbances with balancing moves by other parts than the disturbed part. In its stable overall condition all parts are either in the middle or at the extreme states balancing themselves reciprocally. This internal differentiation constitutes the capability to react self-regulatory to external disturbances: The "Homeostat" is a model for the "law of requisite variety". 18

William Ross Ashby beside the "Homeostat", realised in 1946-47.

Niklas Luhmann´s "autopoiesis" 19 presupposes Ashby´s "law of requisite variety". The evolution of system-internal differentiations improves the capabilities of social, biologic and cognitive systems to react to the environment. 20 Because systems are not as complex as their environment they develop their complexity reducing "selection strategies" 21 for the observation of the environment. These developments presuppose a "requisite variety" emerging in differentiations of "inter system relations". 22

Dr. Thomas Dreher
Schwanthalerstr. 158
D-80339 München.
Homepage with numerous articles on art history since the sixties, a. o. on Concept Art and Intermedia Art.

Copyright © (as defined in Creative Commons Attribution-NoDerivs-NonCommercial 1.0) by the author, October 2011 (German version)/August 2013 (English translation).
This work may be copied in noncommercial contexts if proper credit is given to the author and IASL online.
For other permission, please contact IASL online.

Do you want to send us your opinion or a tip? Then send us an e-mail.

Annotations

1 Bluma: Wiener 2005, p.90s.; Wiener: Cybernetics 1948, p.11ss. back

2 Roch: Shannon 2009, p.43-82,125-144,156-162; Roch/Siegert: Maschinen 1999, p.219,222-229; Wiener: I 1956, p.243-263. back

3 Roch: Shannon 2009, p.145: "Shannon worked out first the answer for the discrete case of a secure communication in `A Mathematical Theory of Cryptography´ (Shannon: Theory 1945), then he prepared the continuous case of a disturbed transmission for `Transmission of Information´ ([manuscript ]1947, [published with the title "Communication in the Presence of Noise": Shannon: Communication 1949]). In 1948 Shannon brought the methods and results of all preparatory works together in `A Mathematical Theory of Communication´ [Shannon/Weaver: Theory 1949/1998]. Shannon problematised not only the question of an effective communication, but concretely the theoretical basics of a secure and effective navigation of electronic air defence systems."
Roch: Shannon 2009, p.104, quoting Shannon: "`When I came out with my paper in 1948, part of that was taken verbatim from the cryptography report, which had not been published at that time.´ [Shannon quoted in Price: Conversation 1985, p.170] For the scientific public Shannon simply devided his 114 pages long `cryptography report´ in two parts: one part more about communication theory and another one on codes."
Cf. Roch: Shannon 2009, p.82,120ss.,128ss.,144s.,159.
Norbert Wiener on feedback and the theory of prediction in its use in antiaircraft fire in the Second World War: Wiener: Cybernetics 1948, p.11-14,23s.,55; Wiener: I 1956, p.249-255,260-265.
On Wiener´s anti-aircraft research and its pioneering role in cybernetics: Bluma: Wiener 2005, p.108ss.,116. back

4 Roch: Shannon 2009, p.57-64. back

5 Roch: Shannon 2009, p.63. Cf. Wiener: Cybernetics 1949, p.20s. back

6 Augarten: Bit 1984, p.109-112,120-131,210ss.,195-202; Gere: Culture 2008, p.46-50,65ss.; Roch: Shannon 2009, p.34; Wiener: Cybernetics 1949, p.22. back

7 Shannon on the reconstructability of languages using stochastics: Bense: Aesthetica 1982, p.335s.; Roch: Shannon 2009, p.26s.; Shannon: Communication Theory 1949, p.656s.; Shannon: Redundancy 1950, p.249; Shannon/Weaver: Theory 1949/1998, p.39-44; Wardrip-Fruin: Media 2007, p.236-239.
Shannon on cryptography: Shannon: Communication Theory 1949. The unpublished "A Mathematical Theory of Communication" of 1945: see ann.3. Cf. Roch: Shannon 2009, p.96-123; Rogers/Valente: History 1993, p.39,42ss. For antiaircraft systems the security of the transmission of control signals was crucial: Roch: Shannon 2009, p.144-152. back

8 Shannon: Redundancy 1950, p.123/248; Wiener: Cybernetics 1949, p.18. back

9 Bense: Aesthetica 1982, p.153,160,211,325; Roch: Shannon 2009, p.115s. back

10 Bense: Aesthetica 1982, p.213. back

11 Cf. Roch: Shannon 2009, p.33s.; Wiener: Cybernetics 1949, p.22s.,139ss. (with comparisons between relais and nerve cells). back

12 Bense: Aesthetica 1982, p.212s.; Porr: Systemtheorie 2002, p.6; Shannon/Weaver: Theory 1949/1998, p.14,32s. back

13 Wiener: Cybernetics 1949, p.13,113-136. back

14 Roch: Shannon 2009, p.160s.; Shannon/Weaver: Theory 1949/1998, p.68. back

15 Bense: Aesthetica 1982, p.364s. back

16 Gregory Bateson and Margaret Mead in Brand: God 1976. back

17 Ashby: Design 1960, p.100-121; Ashby: Introduction 1957, p.73-85. Cf. Wiener: Cybernetics 1949, p.134ss. back

18 Ashby: Introduction 1957, p.202-219; Ashby: Variety 1958; Porr: Systemtheorie 2002, p.11ss. back

19 Luhmann: Systeme 1984, p.60s. back

20 Porr: Systemtheorie 2002, p.13s.,18,41s.,51. Cf. Ashby: Variety 1958, chap. Operational Research. back

21 Luhmann: Systeme 1984, p.47s. back

22 Luhmann: Systeme 1984, p.249. back