IASLonline NetArt: Theorie

Thomas Dreher

Geschichte der Computerkunst

II. Kybernetik
II.1 Grundlagen der Kybernetik

in English

• II.1.1 Ballistik
• II.1.2 Stochastik
• II.1.3 Information
• II.1.4 Feedback
• II.1.5 Homöostase
• Inhaltsverzeichnis
• Bibliographie
• voriges Kapitel
• nächstes Kapitel

Grundlagen der Kybernetik wurden in technischen Modellen demonstriert (s. Kap. II.2). Diese gebauten Modelle wurden grundlegend für die Entwicklung kybernetischer Skulpturen (s. Kap. II.3), während die kybernetischen Grundlagen voraussetzende Informationsästhetik für einige Computergrafiken programmierende Künstler Maßstäbe setzte (s. Kap. III.2). Das zeigt: An einer Einführung in Kybernetik führt kein Weg vorbei.

Norbert Wiener und Claude Elwood Shannon publizierten 1948/49 mit ihren klassischen Schriften zur Kybernetik und Informationstheorie Grundlagen der ballistischen Forschung des amerikanischen Militärs im Zweiten Weltkrieg. Die Flugbahn eines gegnerischen Flugzeugs zu berechnen, setzte voraus, zu wissen, wie Piloten ein Ziel ansteuern. 1 In der Praxis erwies sich, dass die Piloten ihren Anflug mit ihrer Kenntnis vom Verhalten der Flugabwehr änderten, was die Vorausberechnung des Treffpunkts von Flugzeug und Projektil unmöglich machte. 2 Mit dem Problem der Vorhersage dieses Treffpunkts wurde das Problem der Wahrscheinlichkeit, dass eher diese als jene Flugbahn gewählt wird, relevant (s. Kap. II.1.2).

Die Grundlagentexte der Kybernetik waren Resultate der Fliegerabwehrforschung 3, die erst in der Entwicklung von Lenkflugkörpern (Guided Missiles) den Feedback (s. Kap. II.1.4) zwischen Ziel- und Geschossbewegung erfolgreich realisieren wird.

Die Integration von Mathematik in Ingenieurswissenschaften war in der Entwicklung der Ballistik und der Kryptografie in Amerika zunächst umstritten. 4 "Erst 1945 wurde die Rolle der Mathematik in strategischen und technischen Fragen aufgewertet." 5 An Schnittpunkten zwischen Mathematik und Ingenieurswissenschaften bewegten sich Wiener und Shannon vor 1945 und lieferten mit ihren danach publizierten Schriften die Notwendigkeit für einen Aspekte beider Seiten integrierenden Begriff der Information (s. Kap. II.1.3). Für die zeitgleiche Entwicklung von Mainframe Computern plante das amerikanische und britische Militär Anwendungen in Ballistik, Frühwarnungssystemen und Kryptografie. 6

Links: Norbert Wiener (Cover der zweiten Auflage von "Cybernetics", 1962).
Rechts: Claude Elwood Shannon mit "Theseus" (1952) und der Maus, die im Labyrinth den Weg findet (vgl. Kap. II.2.2).
(Credit: MIT Museum, Boston / Nixdorf MuseumsForum, Paderborn)

In der Stochastik werden Wahrscheinlichkeitsrechnungen und Statistiken von Häufigkeiten miteinander verbunden. Die Möglichkeiten der Elemente eines Systems, in Kombinationen mit anderen Elementen zu erscheinen, lassen sich auf Wahrscheinlichkeiten eingrenzen, wenn Statistiken der Häufigkeit ihres bisherigen Vorkommens vorliegen. Bei Vorhersagen ist das wiederholte Vorkommen einer von der Statistik als häufig festgestellten Elementkombination wahrscheinlicher als das einer selten eingetretenen Kombination. Shannon hat die Stochastik auch als Mittel in einem Vorschlag eingesetzt, wie es möglich sein soll, die englische Sprache aus den Häufigkeiten von Elementen und ihren Kombinationen – Buchstaben, Wörter und Wortkombinationen – noch einmal zu entwickeln. Die mittels Computer schnell ausführbaren Kombinationsmöglichkeiten von Schriftzeichen lassen sich durch die Häufigkeit, in der Buchstaben in Einheiten einer zu rekonstruierenden Sprache vorkommen dürfen, einschränken. Im Verlaufe dieses Auswahlverfahrens steigt die Wahrscheinlichkeit, dass die errechneten Möglichkeiten mit der zu rekonstruierenden Sprache übereinstimmen (s. Kap. III.1.3).

Die Annäherung an eine Sprache durch die Rekombination ihrer Elemente mit Rücksicht auf Statistiken der Häufigkeit ihres Vorkommens im Sprachgebrauch erinnert an die Kryptografie: Codes werden durch Vergleiche der dort besonders häufigen Zeichen mit den Zeichen, die in der zu decodierenden Sprache häufig sind, zu entschlüsseln versucht. Für Shannon ergaben sich aus den Verfahren der Kryptografie wiederum die Charakteristika eines nicht entschlüsselbaren Codes: Er darf nur durch Zufallsverfahren entstanden sein, er muss so umfangreich wie der Urtext sein und der Geheimhaltung unterliegen. 7

Mit dem Begriff Information benennen Shannon und Wiener eine Bemessung der Kapazität technischer Systeme. Ein System kann aus technischen Gründen eine bestimmte Informationsmenge übertragen. Diese Bemessung seiner Übertragungskapazität ist von der "semantischen Information" (s. Kap. III.1.3) zu unterscheiden. 8 Grundlegend wurde die wahrscheinliche Verteilung physikalischer Elemente in einem geschlossenen System mit seiner Tendenz zur Entropie ("partikulare Unordnung, Mischung"), wie sie Ludwig Boltzmann in seiner statistischen Thermodynamik entwickelte 9, und ihr Gegenteil, die "Auswahl" und "Entmischung" 10: Information als Negentropie. Aus der Negation der Entropie (Negentropie) wird in der Kybernetik eine Theorie der Information.

Die Alternative zwischen zwei Werten wird als 1 "bit" gemessen. Die Relais von Rechenmaschinen und Computern schalten zwischen zwei Werten "0" und "1". 11 Die Auswahlmöglichkeiten sind 2ⁿ. "n" steht für die Anzahl von Entscheidungen zwischen den Werten "0" und "1". Zu jedem unabhängigen, wählbaren Zeichen gehören "Auswahlwahrscheinlichkeiten" p₁, p₂...p_n. Die Auswahlwahrscheinlichkeit gibt die Wahrscheinlichkeit des Vorkommens eines Elementes an (s. Kap. II.1.2). Die Auswahlwahrscheinlichkeit eines Elementes wird mit dem Logarithmus zur Basis 2 dieser Auswahlwahrscheinlichkeit multipliziert (p_nlog₂p_n). Die so für jede Auswahlwahrscheinlichkeit entstehenden Produkte werden addiert. Die Summe ergibt durch die Negation die Negentropie beziehungsweise die Information "I":

I = - (p₁log₂p₁ + p₂log₂p₂ + ...p_nlog₂p_n)

I = - Σ p_nlog₂p_n (Σ = Summe für n = 1 bis n) 12

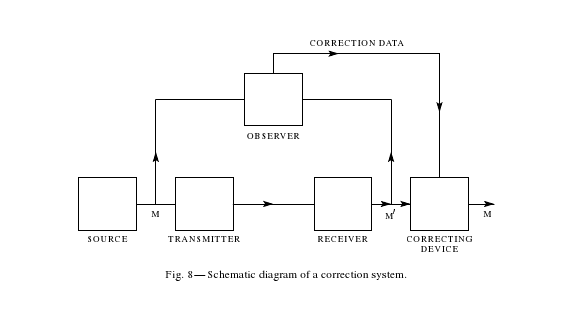
Zur Verarbeitung von Input gehört sowohl die systeminterne Weiterleitung mit Störungen ("noise") als auch die Rückkoppelung des Outputs an das System: Das System kontrolliert den Output, indem es Abweichungen feststellt und auf diese Abweichungen reagiert. Dieser Kontrollvorgang wird als "feedback" 13 bezeichnet und das korrigierende technische Element als "observer". Der "observer" koppelt den Output mit einem die Outputdaten integrierenden Schaltkreis, der den folgenden Output korrigiert. Bei Abweichungen des Outputs oberhalb einer bestimmten Schwelle wird dieser korrigierende "observer" aktiv. 14

Den Zusammenhang zwischen einem System mit internem "observer" und Umwelt rekonstruiert ein "externer Beobachter" 15, den die Kybernetik zweiter Ordnung wiederum als Teil in ein umfangreicheres System integriert. Dieses umfangreichere zweite System enthält die Umwelt des ersten Systems und dessen Beobachter, der sich in dieser Umwelt wahrnehmend-orientierend bewegt. 16 Aus dem externen Beobachter des ersten Systems wird ein interner Beobachter des zweiten umfassenderen Systems.

Shannon, Claude Elwood: A Mathematical Theory of Communication. In: Bell System Technical Journal, Vol. 27/Nr.3, 1948, S. 409.

Ein System kommuniziert mit seiner Umwelt, indem es extern verursachte Störungen intern auszugleichen versucht. William Ross Ashbys kybernetisches Modell einer "Homöostase" (s. Kap. II.2.1) stellt ein System mit einem nach Gleichgewicht strebenden Innenleben vor. 17 Ein vielteiliges System reagiert auf Störungen in einem seiner Teile durch Ausgleichsbewegungen in anderen Teilen. Auf externe Störungen reagiert das mehrteilige System mit seiner internen Variabilität. Im stabilen Gesamtzustand befinden sich in einigen Phasen alle Teile in einer Mittellage oder in entgegengesetzten Grenzzuständen, die sich wechselseitig ausgleichen. Auf dieser Binnendifferenzierung beruht die Fähigkeit, auf Umweltstörungen selbstregulierend reagieren zu können: Der "Homeostat" demonstriert das "Law of requisite variety". 18

William Ross Ashby neben dem 1946-47 realisierten "Homeostat".

Niklas Luhmanns "Autopoiesis" 19 setzt Ashbys "Law of requisite variety" voraus. Die Evolution der systeminternen Ausdifferenzierung verbessert die Fähigkeiten sozialer, biologischer und kognitiver Systeme, auf Umwelt reagieren zu können. 20 Systeme sind nicht so komplex wie ihre Umwelt, sondern sie entwickeln ihre Komplexität reduzierenden "Selektionsstrategien" 21 für die Beobachtung von Umwelt. Diese Entwicklungen setzen in "Intersystembeziehungen" 22 entstandene Ausdifferenzierungen als "requisite variety" voraus.

Dr. Thomas Dreher
Schwanthalerstr. 158
D-80339 München.
Homepage mit zahlreichen kunstkritischen Texte, u.a. zur Konzeptuellen Kunst und Intermedia Art.

Copyright © (as defined in Creative Commons Attribution-NoDerivs-NonCommercial 1.0) by the author, October 2011.
This work may be copied in noncommercial contexts if proper credit is given to the author and IASL online.
For other permission, please contact IASL online.

Wollen Sie dazu Stellung nehmen oder einen eigenen Tip geben? Dann schicken Sie uns eine E-Mail.

Anmerkungen

1 Bluma: Wiener 2005, S.90f.; Wiener: Cybernetics 1948, S.11ff. zurück

2 Roch: Shannon 2009, S.43-82,125-144,156-162; Roch/Siegert: Maschinen 1999, S.219,222-229; Wiener: Ich 1971, S.203-220. zurück

3 Roch: Shannon 2009, S.145: "Shannon arbeitete zuerst in `A Mathematical Theory of Cryptography´ (Shannon: Theory 1945) die Antwort für den diskreten Fall sicherer Kommunikation aus, dann in `Transmission of Information´ ([Manuskript ]1947, [Publikation unter dem Titel "Communication in the Presence of Noise": Shannon: Communication 1949]) die für den kontinuierlichen Fall gestörter Übertragung. 1948 führte er Ergebnisse und Ansätze aller Vorarbeiten zusammen in `A Mathematical Theory of Communication´ [Shannon/Weaver: Theory 1949/1998]. Es ging Shannon hierbei nicht nur um die Frage effektiver Kommunikation, sondern konkret um die theoretischen Grundlagen sicherer und effektiver Steuerung für elektronische Flugabwehrsysteme."
Roch: Shannon 2009, S.104, Shannon zitierend: "`When I came out with my paper in 1948, part of that was taken verbatim from the cryptography report, which had not been published at that time.´ [Shannon nach Price: Conversation 1985, S.170] Shannon teilte seinen 114-seitigen `cryptography report´ für die wissenschaftliche Öffentlichkeit lediglich in zwei Teile: Einen eher Kommunikationstheorie und einen eher Chiffren betreffend."
Vgl. Roch: Shannon 2009, S.82,120ff.,128ff.,144f.,159.
Norbert Wiener über Feedback und Vorhersagetheorie in der Fliegerabwehr durch Flakfeuerleitung im Zweiten Weltkrieg: Wiener: Cybernetics 1948, S.11-14,23f.,55; Wiener: Ich 1971, S.208-214,218ff.,222.
Über Wieners Fliegerabwehrforschung und ihre Vorreiterrolle für die Kybernetik: Bluma: Wiener 2005, S.108ff.,116. zurück

4 Roch: Shannon 2009, S.57-64. zurück

5 Roch: Shannon 2009, S.63. Vgl. Wiener: Cybernetics 1949, S.20f. zurück

6 Augarten: Bit 1984, S.109-112,120-131,210ff.,195-202; Gere: Culture 2008, S.46-50,65ff.; Roch: Shannon 2009, S.34; Wiener: Cybernetics 1949, S.22. zurück

7 Shannon über die Rekonstruierbarkeit von Sprachen mittels Stochastik: Bense: Aesthetica 1982, S.335f.; Roch: Shannon 2009, S.26f.; Shannon: Communication Theory 1949, S.656f.; Shannon: Redundancy 1950, S.249; Shannon/Weaver: Theory 1949/1998, S.39-44; Wardrip-Fruin: Media 2007, S.236-239.
Shannon über Kryptografie: Shannon: Communication Theory 1949. Die unpublizierte "A Mathematical Theory of Communication" von 1945: s. Anm.3. Vgl. Roch: Shannon 2009, S.96-123; Rogers/Valente: History 1993, S.39,42ff. Die Sicherheit der Übertragung von Steuersignalen war für Feuerleitsysteme entscheidend: Roch: Shannon 2009, S.144-152. zurück

8 Shannon: Redundancy 1950, S.123/248; Wiener: Cybernetics 1949, S.18. zurück

9 Bense: Aesthetica 1982, S.153,160,211,325; Roch: Shannon 2009, S.115f. zurück

10 Bense: Aesthetica 1982, S.213. zurück

11 Vgl. Roch: Shannon 2009, S.33f.; Wiener: Cybernetics 1949, S.22f.,139ff. (mit Vergleichen zwischen Relais und Nervenzellen). zurück

12 Bense: Aesthetica 1982, S.212f.; Porr: Systemtheorie 2002, S.6; Shannon/Weaver: Theory 1949/1998, S.14,32f. zurück

13 Wiener: Cybernetics 1949, S.13,113-136. zurück

14 Roch: Shannon 2009, S.160f.; Shannon/Weaver: Theory 1949/1998, S.68. zurück

15 Bense: Aesthetica 1982, S.364f. zurück

16 Gregory Bateson und Margaret Mead in Brand: God 1976. zurück

17 Ashby: Design 1960, S.100-121; Ashby: Introduction 1957, S.73-85. Vgl. Wiener: Cybernetics 1949, S.134ff. zurück

18 Ashby: Introduction 1957, S.202-219; Ashby: Variety 1958; Porr: Systemtheorie 2002, S.11ff. zurück

19 Luhmann: Systeme 1984, S.60f. zurück

20 Porr: Systemtheorie 2002, S.13f.,18,41f.,51. Vgl. Ashby: Variety 1958, Kap. Operational Research. zurück

21 Luhmann: Systeme 1984, S.47f. zurück

22 Luhmann: Systeme 1984, S.249. zurück