IASLonline NetArt: Theorie

Thomas Dreher

Geschichte der Computerkunst

III. Informationsästhetik
III.2 Computergrafik

in English

• III.2.1 Analoggrafik
• III.2.2 Digitale Computergrafik
• Inhaltsverzeichnis
• Bibliographie
• voriges Kapitel
• nächstes Kapitel

Der Einsatz von Großrechnern zur Textgenerierung (s. Kap.III.1) liefert eine Vorgeschichte zur Computergrafik (s. Kap. III.2.2). Eine weitere Vorgeschichte ergibt sich aus künstlerischen Anwendungen von Kathodenstrahloszillographen, die als Kontrollanzeige in der Elektrotechnik und als Ausgabemedium von Analogcomputern eingesetzt wurden.

Laposky, Benjamin Francis: Oscillon Number Four, 1950, Foto vom Bildschirm eines Oszillographen.

Benjamin Francis Laposky fotografierte ab 1950 den Bildschirm seines modifizierten Oszillographen, den er unter anderem mit Sinuswellengeneratoren kombinierte. Die begrenzte Vielfalt der Wellenformen des Oszillographen erweiterte Laposky um "other electrical and electronic circuits...to create the almost infinite variety of forms." Laposky selbst stellte den Bezug seiner "electronic abstractions" 1 zur Computerkunst her:

The relationship of the oscillons to computer art is that the basic waveforms are analogue curves of the type used in analogue computer systems. 2

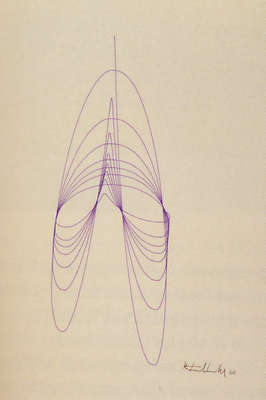
Franke, Herbert W.: Oszillogramme, 1956, Fotos vom Bildschirm eines Oszillographen.

Franke, Herbert W./Raimann, Franz: Analogtechnik zur Steuerung von Elektronenstrahlen in einem Oszilloskop. Fotografiert am 13.8.2014 in Puppling bei Egling/Bavaria. Foto: Thomas Dreher.

Herbert W. Franke realisierte 1955/56 "Pendeloszillogramme" mit einer vor dem Bildschirm des Oszillographen bewegten Contaflex-Spiegelreflexkamera. Der Bildschirm zeigte Kurven. Zur Erzeugung dieser Kurven baute Franz Raimann für Franke "ein einfaches Analogrechensystem..., dazu geeignet, die elementaren Kurven zu berechnen...Die Art der Überlagerung [von komplizierten Kurven] ließ sich mit Hilfe eines Mischpultes in Echtzeit einstellen." 3 Der Mischpult ermöglichte Modifikationen der Bewegung des Elektronenstrahls in der Horizontal- und Vertikalachse. Normalerweise wird in Oszillographpen eine horizontale Grundlinienbewegung vertikal abgelenkt. Mit Raimanns Analogrechensystem liessen sich Bewegungen auf der Horizontal- und Vertikalachse abhängig von der Zeitdimension einstellen.

Wie Schöffer in "CYSP I" (1956, s. Kap. II.3.1.2) einen kleinen, von Philips für ihn gebauten Rechner vor den in den sechziger Jahren aufkommenden Minicomputer einsetzt, so setzte auch Franke einen für seine Zwecke gebauten kleinen Rechner ein. Dieser Rechner war mit einem Oszillographen verbunden, "dessen Bildschirm leider nur einen Radius von fünf Zentimetern hatte und dick gezeichnete Linien hervorbrachte. Um überhaupt brauchbare Bilder zu erreichen, versuchte ich alles Mögliche und hatte schließlich die besten Resultate, wenn ich die Kamera im verdunkelten Raum mit geöffneter Blende vor dem Bildschirm bewegte...Um eine gleichmäßige Bewegung zu erreichen, befestigte ich sie dazu bei den ersten Versuchen wie bei einem Pendel an einer Schnur, erzielte allerdings die schließlich besten Resultate durch eine gleichmäßige freihändige Bewegung – das ließ sich richtig üben und lernen. Die Bilder zeigen die Überlagerung der Kurven als gitterartige, oft räumlich wirkende Struktur." 4 Die in Echtzeit auf dem Bildschirm des Oszillographen erzeugten Kurven dokumentierte Franke nicht einfach als Fotoreproduktion, sondern erzielte Strukturen mit visueller Tiefenwirkung durch die mit geöffneter Blende bewegte Kamera. Die Gestaltungseinschränkungen, die der Bildschirm seines Oszilloskops mit seinen "dick gezeichneten Linien" mit sich brachte, überwandt Franke, indem er die Kamera vor dem Bildschirm bewegte und dabei die Entfernung veränderte: Dicht aufeinander folgende Linien und Überlagerungen wurden so möglich.

Fuchshuber, Roland K.: Links: Rocker, 1960, Plotterzeichnung.
Rechts: Polstelle, 1960, Plotterzeichnung.

Roland K. Fuchshuber wurde 1960 Mitglied der Gründungskommission des Centre Européen de Traitement de l´Information Scientifique (CETIS). Bei Euratom (Europäische Atomgemeinschaft) in Brüssel und Ispra (Italien) begann Fuchshuber, Grafiken mit PACE-Analogrechensystemen von Electronic Associates Incorporated (EAI) zu erstellen. Der "Klirrfaktor eines Verstärkers" beeinflusste den Verlauf von parallelen Kurvenlinien, die als Plotterzeichnungen erhalten sind. 5

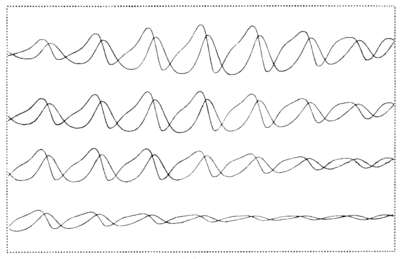
Alsleben, Kurd/Passow, Cord: Computergrafik 4, 1960,
Plotterzeichnung (Alsleben: Redundandanz 1962, S.52, Abb.d).

Der Künstler Kurd Alsleben und der Physiker Cord Passow verwendeten 1960/61 einen Analogrechner des Deutschen Elektronen Synchotron (DESY) in Hamburg (EAI 231 R), um Wellen zu erzeugen, die sowohl in Reihen untereinander als auch sich überlagernd von einem Plotter gedruckt wurden. So entstanden fünf von einem Plotter ausgeführten Computergrafiken. Eine dieser Plotterzeichnungen weist vier Zeilen auf. Jede Zeile besteht aus zwei sich überlagernden Wellenlinien. Den Verlauf der Wellenlinien bestimmende "Parameterveränderungen" wurden mit Potentiometern erzeugt. 6

Ein elektronischer Analogrechner erlaubte Echtzeitmanipulationen über Steckfelder und Potentiometer (s. Kap. III.2.1) – anders als die von Béla Julesz, A. Michael Noll (ab 1962), Frieder Nake (ab 1963) und Georg Nees (ab 1964) eingesetzten digitalen Großrechner, die erst nach dem Rechenprozess durch Plotter das Ergebnis des (über Lochkarten oder Magnetspeicher eingegebenen) Programms zu sehen gestatteten. Programmiert wurde mit FORTRAN oder ALGOL, den höheren Programmiersprachen für Compiler. Compiler übersetzen Programmiersprachen in Maschinensprachen. Compiler erleichterten erst seit wenigen Jahren 7 die Programmierung, die vorher nur in Maschinensprache möglich war.

A. Michael Noll, Georg Nees und Frieder Nake schufen in den sechziger Jahren frühe digitale Computergrafik. Sie nahmen Verfahren der in Kap. III.1 vorgestellten Beispiele der Computerliteratur, vor allem von Christopher Strachey (s. Kap. III.1.2) und Theo Lutz (s. Kap. III.1.3), auf:

• a. die Auswahl weniger Elemente, die in einem Archiv gespeichert wird,
• b. eine Kombinationssyntax,
• c. einen Zufallsgenerator,
• d. Bestimmung der Häufigkeit, in der das Programm auf Elemente zugreifen kann.

Wenn als Grundelemente nicht Textzeichen, sondern geometrische Elemente eingesetzt werden, dann verschiebt sich die künstlerische Arbeit auf die Schaffung von Gebilden, die – so das von der Informationsästhetik formulierte Ziel – für die Wahrnehmung der ganzen Fläche und in den Relationen zwischen einzelnen Elementen sowohl hinreichend komplex als auch nicht zu komplex sind. Das ergibt folgende Abweichungen der Computergrafik von Computerliteratur:

• zu a. Das Wortarchiv wird von Elementen – vor allem Linien – ersetzt, welche die Programmiersprache konstituiert (z. B. Linien als Verbindungen zwischen Punkten).
• zu b. Lage und Länge der Grundelemente auf der Fläche können in einer von der Kombinationsweise bestimmten Art variieren, welche statt der Links-Rechts- und Oben-Unten-Gliederung von Textzeichenkombinationen in Zeilen die Fläche als Ganze strukturiert. Die Zeilengliederung ersetzt zum Beispiel eine Flächengliederung in Zonen, in denen das Programm neu startet.
• zu c. Da sich der Zufallsgenerator nicht nur in der Auswahl von Elementen, sondern auch in der Modifikation der Kombinationsweise von Zone zu Zone auswirkt, bestimmt die Bandbreite dieser Variationen wiederum den Gesamteindruck eines Werkes.
• zu d. Die Begrenzung der Häufigkeit des Zugriffs betrifft nicht nur die Auswahl von Einzelelementen, sondern auch die Kombinationsweisen mit Folgen für die Gesamtansicht statt für einzelne Sätze in einem Satzensemble. Die Relationen zwischen programmierter Flächengliederung und den optischen Effekten der Gesamtansicht ersetzen die Lesbarkeit der Sätze und/oder Zeilen eines Textes. 8

Bevor frühe Beispiele der digitalen Computergrafik vorgestellt werden, welche die oben genannten Kriterien erfüllen, sollen die Ziele der Informationsästhetik kurz skizziert werden, die vor allem Georg Nees und Frieder Nake beeinflussten.

In der Informationsästhetik werden die Relationen zwischen Programmstruktur und visueller Wahrnehmung thematisiert. Max Bense und Abraham André Moles bestimmen das "ästhetische Maß" über die für Rezipienten bestmögliche Relation zwischen "Komplexität" der wahrnehmbaren "Information" und der dabei zu entdeckenden "Ordnung" ("Redundanz"): Bense bestimmt das ästhetische Maß mit George David Birkhoff als Ordnung dividiert durch Komplexität ("Birkhoffscher Quotient"). 9 Moles dagegen zieht Verhältnisse vor, welche der Multiplikation Ordnung mal Komplexität entsprechen und beruft sich dabei auf empirische Untersuchungen. 10

Grundlage dieser numerischen Bestimmung des "ästhetischen Maßes" ist Shannons "statistische Information". 11 Sie setzt exaktes Wissen über die Anzahl von Elementen ("Zeichenrepertoire") und ihre Kombinationsmöglichkeiten voraus. 12 Deshalb liefern konkret-serielle und programmierte Kunst Modellfälle für Informationsästhetik.

Nach Bense realisiert die Kunst unwahrscheinliche Ordnungen durch "Ausscheidung des Vermeidbaren" und "Verringerung der Redundanz". 13 Während Bense Eigenschaften der Kunstwerke erörtert, thematisiert Moles ihre Wahrnehmung. Die "Apperzeptionsgrenze" des Empfängers und ihre Abhängigkeit von seiner Vorkenntnis stehen im Zentrum von Moles Überlegungen. Über der "Apperzeptionsgrenze" kann in visueller Vielfalt keine Ordnung mehr erkannt werden, weshalb diese Grenze nicht überschritten werden soll. 14 Ein gewisses Maß an Redundanz bleibt also unabdingbar. Im Gegensatz zu John Cages nicht-normativer Ästhetik der simultanen Zufallsoperationen 15 expliziert die Informationstheorie ein objektivierbares ästhetisches Ziel: die nach ästhetischen Gesichtspunkten beste Relation zwischen Information und Redundanz.

Götz, Karl Otto: Statistisch-metrischer Versuch 4:2:2:1, Entwurf Sommer 1959, Ausführung mit Bleistift und Filzschreiber auf Karton 1960. Foto: Kukulies. Sammlung Etzold. Städtisches Museum Abteiberg. Mönchengladbach (Kersting: Sammlung Etzold 1986, S.206).

Der als informeller Maler und Mitglied der Gruppe Quadriga in den fünfziger Jahren bekannt gewordene Karl Otto Götz experimentierte 1959 bis 1961 in "statistisch-metrischen Modulationen" mit Raster aus schwarzen und weißen Rechtecken, die noch manuell ausgeführt wurden.

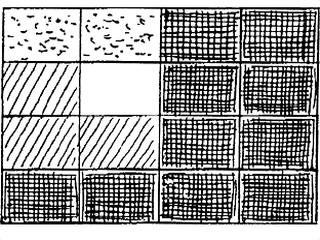
Karl Otto Götz vor Density 10:3:2:1, 1961, Filzstift und Tusche auf Bristolkartons, aufgezogen auf Leinwand (Götz: Erinnerungen 1983, S.900, Ill.1016).

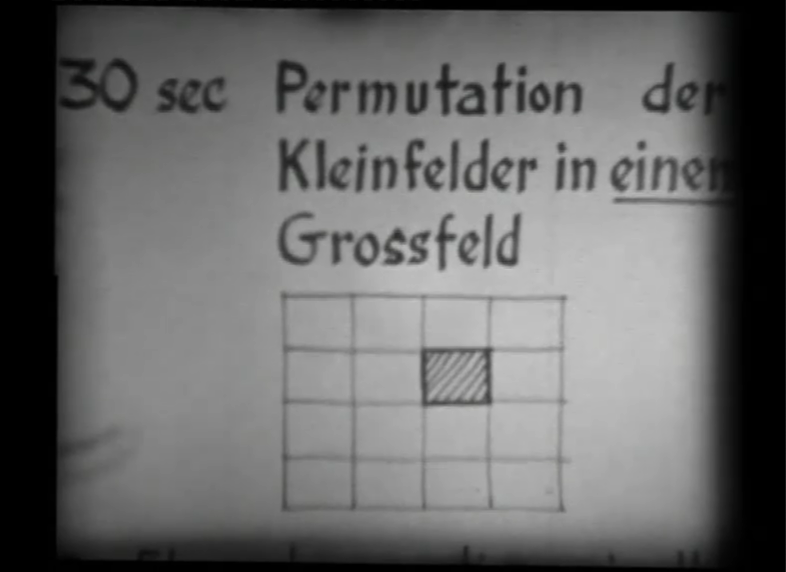
In "Density 10:3:2:1" (1961) gliedert Götz die "Bildfläche (200 x 260 cm)" in "16 Superfelder", die wiederum in "16 Großfelder" gleicher Größe unterteilt werden und bestimmt die Häufigkeit, in der schwarze Felder (bei den "2 Helligkeitsgraden" schwarz und weiß) vorkommen, in den vier "Dichtegraden", die der Titel angibt. Die Grundeinheit ist ein Raster aus vier mal vier Rechtecken ("16 Großfelder" mit je 16 "Kleinfeldern"). Eines dieser 16 Rechtecke ist weiß (Dichtegrad "sehr hell") und 10 sind schwarz (Dichtegrad "dunkel"). In den beiden Dichtegraden zwischen schwarzen und weißen Rechtecken sind 2 Rechtecke heller ("geringe Dichte") und 3 Rechtecke dunkler ("mittlere Dichte"). Der Titel "Density 10:3:2:1" bezeichnet also 10 mal Dichtegrad "dunkel", 3 mal "mittlere Dichte", 2 mal "geringe Dichte" und ein Mal Dichtegrad "sehr hell".

Götz, Karl Otto: Density 10:3:2:1, Skizze, 1961, Einteilung der Bildfläche in Superfelder mit vier verschiedenen Dichtegraden (Götz: Malerei 1961, S.14).

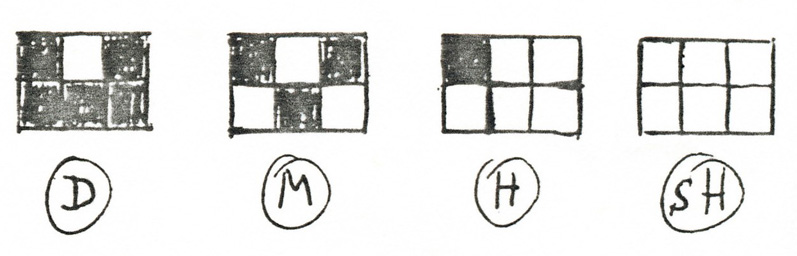
Götz veranschaulicht die Realisierung der vier Dichtegrade an einem Raster aus 2 x 3 Quadraten: Von den sechs Quadraten sind mit ansteigender Dichte kein Feld ("sehr hell"), ein Feld ("geringe Dichte"), drei ("mittlere Dichte") und fünf Felder schwarz ("dunkel"). Der hellere und der dunklere Ton von Feldern ergibt sich aus der Anzahl von per Zufall verteilten schwarzen und weißen Elementen: "statistische Mengenverhältnisse".

Götz, Karl Otto: Density 10:3:2:1, Skizze, 1961, Kleinfelder mit vier verschiedenen Dichtegraden: D = dunkel, M = mittlere Dichte, H = hell, sH = sehr hell (Götz: Malerei 1961, S.23).

Die auf 16 Superfelder verteilten 16 x 16 (=256) Großfelder ergeben ein Feld, durch dessen unterschiedlich dichte Verteilung von schwarzen und weißen Elementen der Blick in verschiedene Richtungen gleitet und Anhaltspunkte bei markanten, besonders dichten schwarzen oder weißen Feldern sucht. Die Aufteilung in "Großfelder" wird an horizontalen und vertikalen Bruchlinien zwischen Zonen mit einerseits dominant schwarzen und andererseits dominant weißen Quadraten erkennbar.

Studenten konnten ihren Bereich auf "vorgerasterten Zeichenkartons" zu Hause mit Filzstift und Tusche ausführen. Danach wurde das Rasterbild aus den in Arbeitsteilung erstellten "Kartons auf Leinwand montiert." Die so realisierten "ca. 400.000 Bildpunkte (Elemente)" ergeben nach Götz ein "Modellbild", das als "elektronisches Fernsehbild" ausführbar wäre. Die "2 Helligkeitsgrade" von Götzs "Modellbildern" wären durch die "etwa 40 Helligkeitsstufen" des Fernsehbildes mit "450.000 Bildpunkten" zu ersetzen.

Als Götz 1960 versuchte, Siemens für die Realisierung seiner "Rasterbilder" zu gewinnen, traf er auf wenig Interesse und scheiterte. 1962 entstand der Film "Density 10:2:2:1" (8 mm) aus fotografierten Permutationen der Teile eines "Rasterbildes". Zwischentitel geben an, welche Rasterelemente – "Bausteine in Kleinfeldern", "Kleinfelder", "Großfelder" – ausgetauscht wurden. Götz fotografierte diese Permutationen. Die Fotografien bilden die Einzelbilder des Films. Die durch die Filmprojektion bewegten Einzelbildsequenzen aus Rasterpermutationen erwecken den Eindruck eines flimmernden Bildes. Während die Permutationen von den kleinsten "Bausteinen" zu den "Großfeldern" fortschreiten, werden im Verlauf des fast drei Minuten langen Films die Unterschiede deutlicher.

Götz, Karl Otto: Density 10:2:2:1, 1962, Film, 8 mm (Claus: Zeitalter 2008).

Götz errechnete den "Informationsgehalt" seiner Bilder. Dass ein hoher "Gesamtinformationsgehalt" und geringe "Redundanz" das Ergebnis seiner Berechnungen waren, überrascht nicht angesichts der Probleme für Beobachter, Ordnung in den Relationen zwischen den Rechtecken zu erkennen. Götz betrieb "informationstheoretische Betrachtung" und die Erforschung "gestaltpsychologische[r] Werte" separat. 16

Götz nimmt in einer noch manuellen Ausführung Algorithmen der digitalen Computergrafiken vorweg: Die Reduktion auf wenige Elemente, Kombinationsregeln und von Häufigkeitsregeln begrenzte Auswahlmöglichkeiten in der Realisierung sind Aspekte der Informationsästhetik, die in Computergrafiken wiederkehren.

Der Elektroingenieur Béla Julesz promovierte 1956 in Budapest an der Ungarischen Akademie der Wissenschaften. Nach dem Einmarsch der Armee der Sowjetunion in Ungarn emigrierte er nach Amerika. Einige Wochen nach seiner Ankunft in den Vereinigten Staaten wurde Julesz in das technische Forschungsteam der Bell Laboratories in Murray Hill/New Jersey aufgenommen. 17

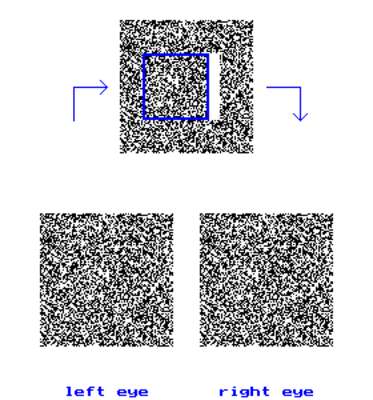
Julesz, Béla: Stereopsis, 1959, Plotterzeichnung.

1960 publizierte Julesz seine Untersuchungen zur "Binocular Depth Perception of Computer-Generated Patterns" in "The Bell System Technical Journal". Der Ausgabe des "Technical Journal" lag eine Brille bei, mit der die Random-Stereogramme gesehen werden konnten, die in Julesz´ Beitrag abgebildet sind: Diese Brille ist ein Vorläufer der LC-Stereobrillen. 18 Ein Mainframe Computer IBM 704 (1954-60) errechnete pro Stereogramm Bilder aus 10.000 Punkten. Ein Pseudo-Zufallsgenerator verteilte 16 Helligkeitswerte. 19 Die beiden von einem Plotter ausgedruckten und nebeneinander publizierten Rechtecke mit der gleichen Zufalls-Punkte-Verteilung wichen in der Mittelzone voneinander ab: Je ein identisches Quadrat erschien links und rechts seitlich versetzt ("parallax shift"). Die Abweichungen betreffen also eine versetzte quadratische Zone und ihre Umgebung. 20 Diese Parallaxe provoziert in der binokularen Wahrnehmung mit Brille Dreidimensionalität, wobei keine Eigenschaft der Bilder des Stereogramms eine Auflösung durch Sehmuster für dreidimensionale Körper nahelegt.

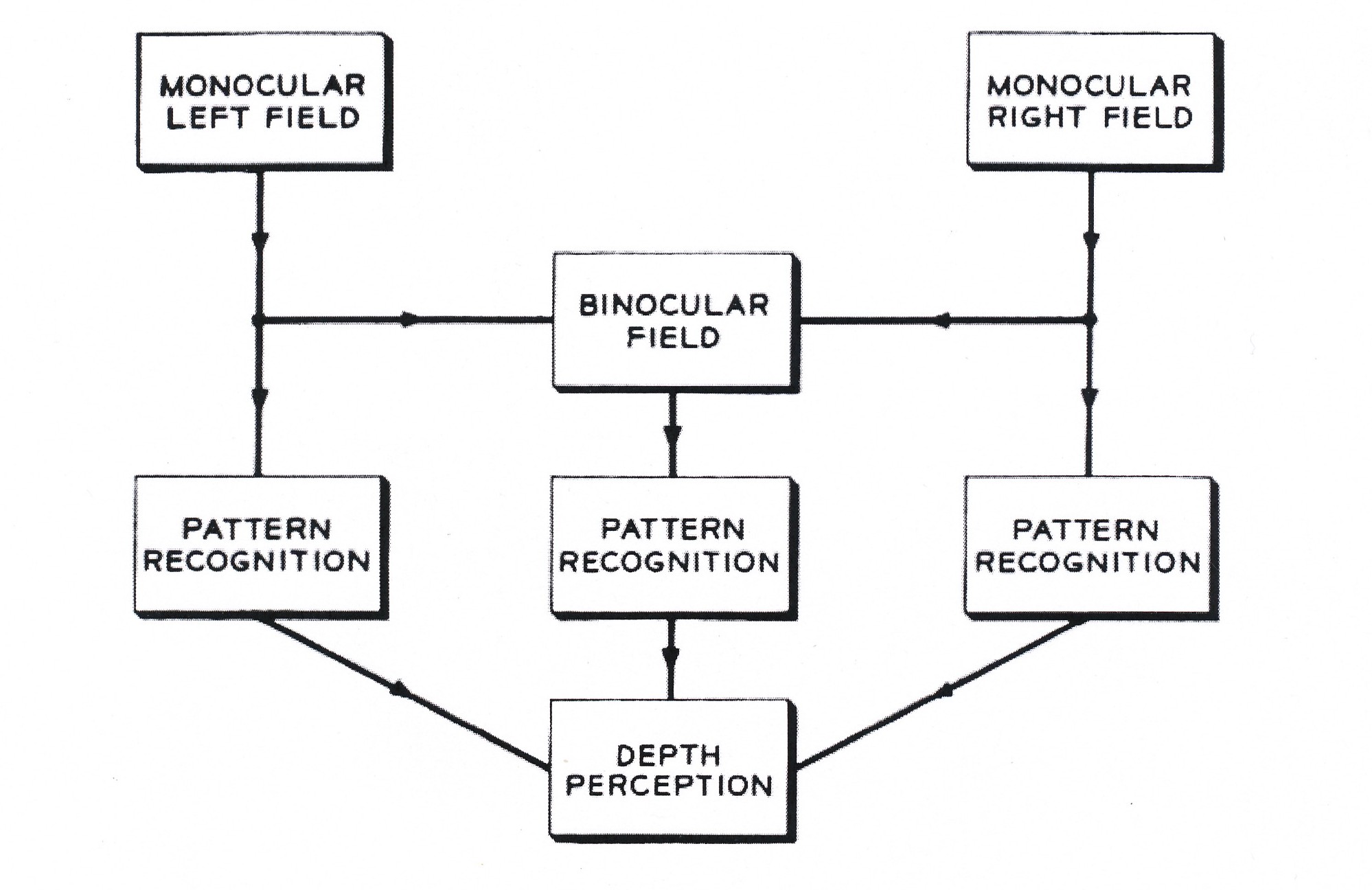
Julesz, Béla: Depth perception by monocular and binocular pattern recognition, 1960 (Julesz: Depth Perception 1960, S.1128, Fig.3).

Julesz erkennt eine genuin "binocular pattern recoginition", die keine "monocular pattern recognition" voraussetzt und eigenen Gesetzen folgt. 21 Tiefenwahrnehmung kann zwar durch "binocular pattern recognition" allein entstehen, ist aber auch als "combination of binocular and monocular pattern recognition" möglich: "Monocular macropattern recognition" verstärkt die Tiefenwirkung. 22 Julesz´ Untersuchungen des "zyklopischen Sehens" demonstrieren, dass mit einem Auge erkennbare Sehmuster und binokuläre Sehmuster in der Tiefenwahrnehmung zusammengeführt werden. Julesz´ Forschungen hatten Konsequenzen für die Wahrnehmungspsychologie, die Kognition und die Entwicklung von Einzelbild- bzw. Autostereogrammen. 23 1965 wurden Julesz´ Wahrnehmungsexperimente mit A. Michael Nolls Computergrafiken in der New Yorker Howard Wise Gallery ausgestellt. 24

A. Michael Noll schloß sein Studium am Newark College of Engineering 1961 mit dem B.S.E.E. (Bachelor of Science in Electrical Engineering) ab. 1961 bis 1971 arbeitete er in einer Abteilung der Bell Laboratories (Murray Hill/New Jersey) für Telefonübertragungen. 25

Im Sommer 1962 entstanden auf einem IBM 7090 (ab 1959) der Bell Labs in FORTRAN programmierte "Patterns", die Noll noch nicht als Kunst verstanden wissen wollte. 26 Die Resultate der Rechenprozesse zeigte ein Stromberg Carlson 4020 Microfilm-Plotter als Elektronenkonfigurationen auf einer Kathodenstrahlröhre. Der Rechenprozess führt über einen "Decoder and Command Generator" zur Erzeugung des Bildes auf dem Bildschirm. Nolls FORTRAN-Code enthielt auch Befehle für den Microfilm-Plotter, die weitere "subroutines " aufriefen. Der Bildschirm wurde fotografiert und das 35 mm Negativ "im Fotodruck-Verfahren in unterschiedlichen Größen vervielfältigt." 27

Zwischen mittels "White Noise Generator" plazierten Punkten wurden Linien durch programmierte Verbindungen erzeugt. Die verschieden langen Linien fügten sich zu einer gezackten Linie.

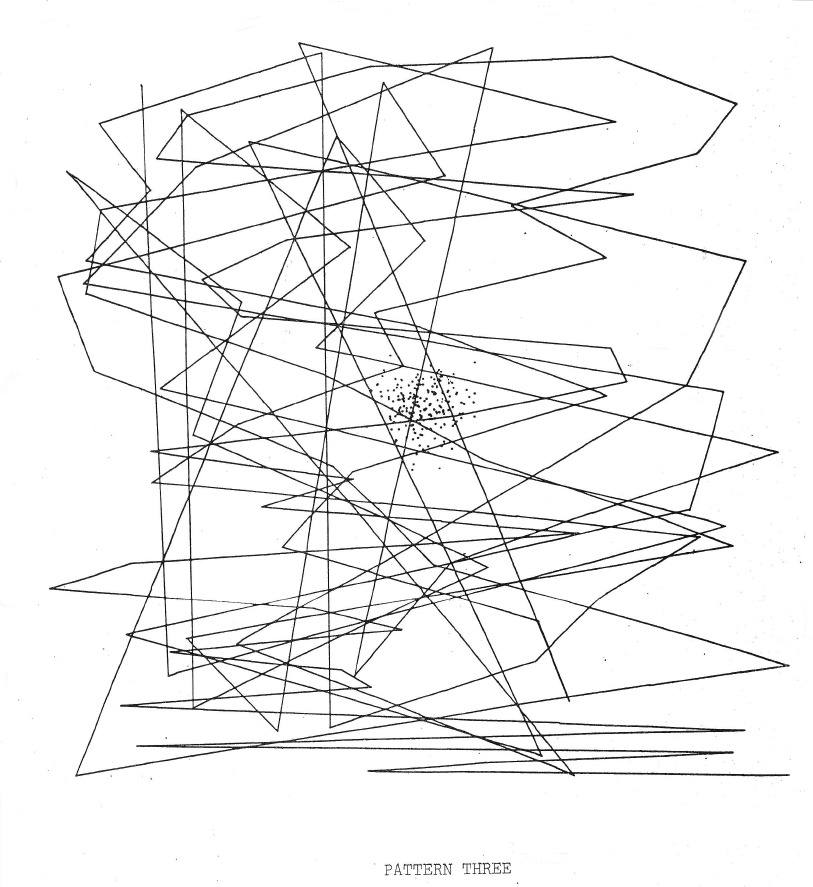
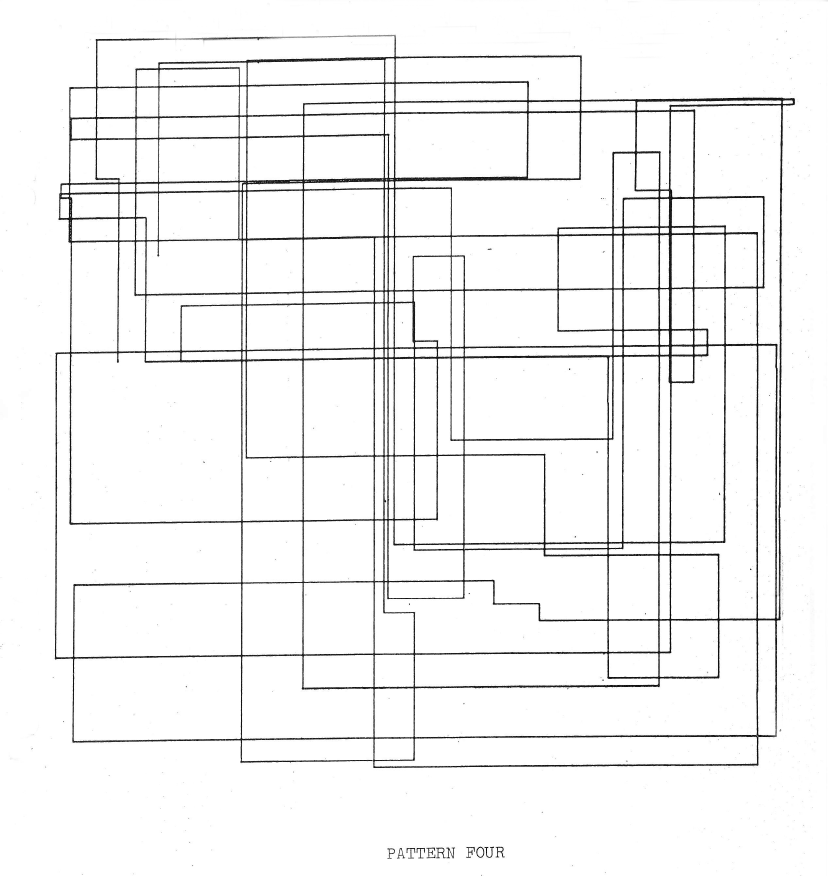
Noll, A. Michael: Links: Pattern Three, 1962, Fotodruck.
Rechts: Pattern Four, 1962, Fotodruck (Noll: Patterns 1962, o.P.).

Die Programmierung der Punktewolken, die in "Pattern One", "Two" and "Three" auf den gezackten Linien erscheinen, erfolgte um einen zentralen Punkt herum. Die Werte der auf x- und y-Achsen horizontal und vertikal plazierten, in einer Zufallsprozedur ermittelten Punkte zur Lokalisierung von Linien wurden für "Pattern Four" und "Pattern Five" "alternately repeated to make the lines horizontal und vertical." Die alle Punkte verbindende Linie wechselt die Richtung ausschließlich im rechten Winkel. In "Pattern Four" sind die beiden Enden der Linie in von ihr ausgegrenzten Feldern erkennbar. 28

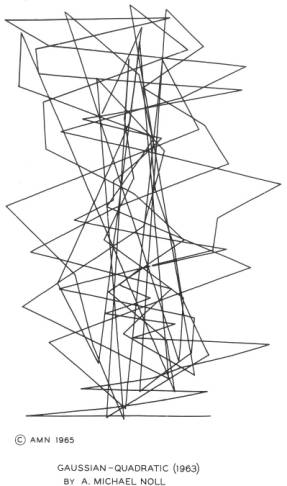
Noll verteilt in "Gaussian Quadratic" (1962/63) 100 Punkte in der Vertikal- und Horizontalachse nach verschiedenen Kriterien: Die Situierung in der Horizontalen folgt der Normal- oder Gauß-Verteilung, während die vertikale Lokalisierung einer Gleichung folgt:

The vertical positions increase quadratically, i.e., the first point has a vertical position from the bottom of the picture given by 1² + 5x1, the second point 2² + 5x2, the third point 3² + 5x3, etc. 29

Um zu vermeiden, dass Punkte außerhalb der festgesetzten Blattgröße liegen, wurde die Vertikalverteilung des oberen Blattrandes unten gespiegelt. Die Gauß-Verteilung in der Horizontalen folgt der Standardnormalverteilung. Die Verbindung der Punkte zu 99 Linien ergibt ein vertikales Mittelfeld mit mehrfach sich kreuzenden Linien. Diese Linien bilden aber auch eine Zickzack-Linie mit zufälligen Richtungswechseln und einigen auffallenden Ausschlägen nach beiden Seiten. Die Zickzack-Linie erscheint als ein vertikales Gebilde, das auf der als Grund dienenden untersten horizontalen Linie balanciert.

Noll, A. Michael: Gaussian Quadratic, 1962/63, Fotodruck.

Noll verfolgt auch in "Gaussian Quadratic" die Strategie der zufälligen Richtungswechsel der Linie vieler "Patterns". Er erweitert die algorithmischen Kriterien so, dass die Relationen von Ordnung und Zufall in der Linienkonfiguration die Wahrnehmung auf der Suche nach dem "ästhetischen Maß" stärker herausfordern. 30

Frieder Nake bezeichnet die von Noll 1962 realisierten "Patterns" als "Polygonzüge". 31 "Polygonzüge" von Georg Nees erschienen im Dezember 1964 in Heft 3/4 der "Grundlagenstudien aus Kybernetik und Geisteswissenschaft". 32 Das in ALGOL geschriebene Programm führte ein Großrechner Siemens 2002 (1959-66) aus. Ein Zuse Z64 Graphomat druckte das Resultat.

Nees, Georg: 23-Ecke, 1964, Plotterzeichnung (Nees: Grundlagenstudien 1964, S.124, Bild 2).

Die Polygonzüge erscheinen vielfach neben- und untereinander. Der Algorithmus startet in vom Programm vorgegebenen Feldern bzw. "Matrizen" 33 neu und legt die Verteilung von aufeinander folgenden Linien per Zufallsgenerator fest. Die Anzahl der Linien pro "Matriz" ist im Programm festgelegt.

Nees, Georg: Ohne Titel (Mikroinnovation), 1967, Plotterzeichnung (Nees: Computergraphik 2006, S.222, Bild 31).

In einer 1965-68 realisierten Serie von Computergrafiken bestimmt Nees, wie weit die Felder, in denen das Programm die Linienkonfiguration neu startet, von den "Polygonzügen" überschritten werden dürfen. 34 Da die "Matrizen" in geringen Abständen aufeinander folgen, durchdringen sich die sie überschreitenden "Polygonzüge". Sie erscheinen dem flüchtigen Blick als komplexes Liniengewirr. 35 Die Zusammensetzung des Gewirrs aus schräg und rechteckig aufeinander zulaufenden Linien erschließt sich erst im Nahblick, also in einer Rekonstruktion der Relationen zwischen den Linienkonfigurationen. In der Gesamtansicht ergeben sich Zonen dichterer Überlagerungen und in und über Zonen hinweg dominierende Linienrichtungen.

Von Werk zu Werk variieren die Relationen zwischen Komplexität durch Vielheit (durch die Unterteilung in "Matrizen" und durch Überlagerungen von Linienkonfigurationen) und Einfachheit durch eine Strukturierung, zu der ein die ganze Fläche überschauender Wahrnehmungsprozess provoziert wird. 36 Die Grafiken von Georg Nees erweisen sich als Modelle für die Frage nach Vermittlungen von "Ordnung und Komplexität" 37 im "ästhetischen Maß".

Auf der Suche nach Ähnlichkeiten und Wiederholungen, die eine visuelle Schemabildung erleichtern – oder informationstheoretisch gesprochen: die das Erkennen von Ordnung durch Redundanz (als Wiederkehr des Gleichen) ermöglichen – wird die Bildfläche von Beobachtern immer wieder neu fokussiert. Nees spricht von einer "Gradation vom Typus Haufen–Variation–Gestalt". 38 Die "Mikroästhetik" des Produzierten – bestimmt von der "Texturerzeugung durch Überlappung" 39 – und die "Makroästhetik" der kognitiven Auflösung in refokussierender Wahrnehmung bilden aufeinander verweisende Ebenen: "Gestalten sind ästhetische Informationseinheiten mit Lokal- und Distalnexus." 40

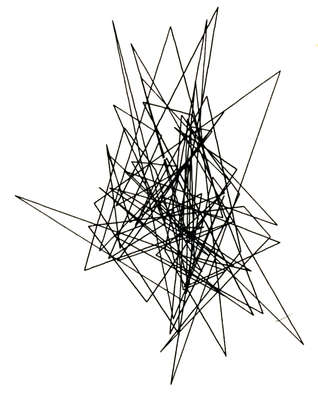
Nake, Frieder: Zufälliger Polygonzug, 1963, Plotterzeichnung, 10 x 10 cm (Nake: Ästhetik 1974, S.19, Abb.5.2-7)/1964, Plotterzeichnung, 15,5 x 11,5 cm (Herzogenrath/Nierhoff-Wielk: Machina 2007, S.424, Nr.259).

Frieder Nake entwickelte ab 1963/64 das Übersetzungsprogramm Compart ER 56 in Maschinensprache, um über den Großrechner Standard Electric Lorenz (SEL) ER 65 (ab 1959) den vom Rechenzentrum Stuttgart neu angeschafften Zeichentisch Zuse Z64 Graphomat steuern zu können. 1963 erstellte Nake mit seinem neuen Programm "zufällige Polygonzüge" aus Linien, die mittels "Pseudo-Zufallsgenerator" gesetzte Punkte verbinden. Nake realisierte diese Werke nach Nolls und offenbar vor Nees´ Polygonzügen. 41

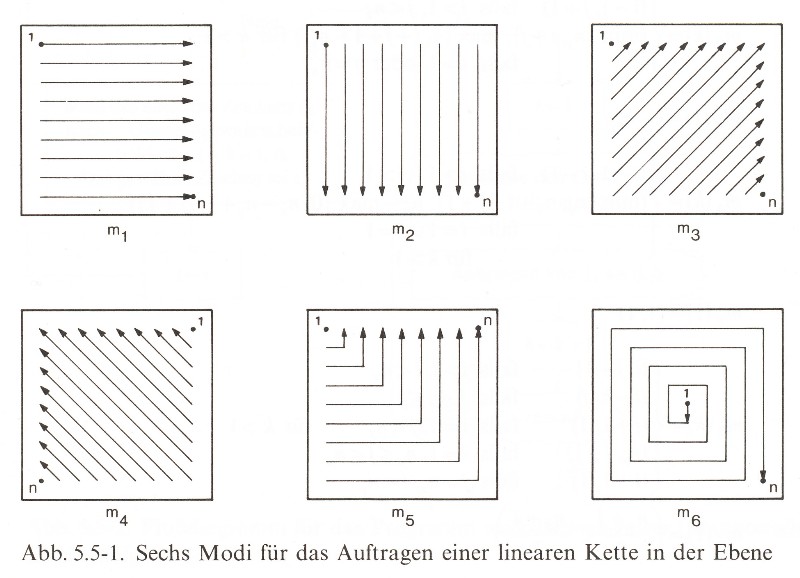
Nake, Frieder: Walk-Through-Raster, 1966, Sechs Modi (Nake: Ästhetik 1974, S.229, Abb. 5.5-1).

Das Programm "walk-through-raster" schrieb Nake 1966 in "ALGOL60 (mit einigen Assembler-Unterprogrammen)". Ein Lochstreifen enthielt die Anweisungen für einen Telefunken TR4 (ab 1962) der Universität Stuttgart, dessen Resultate ein Zuse Z64 Graphomat druckte.

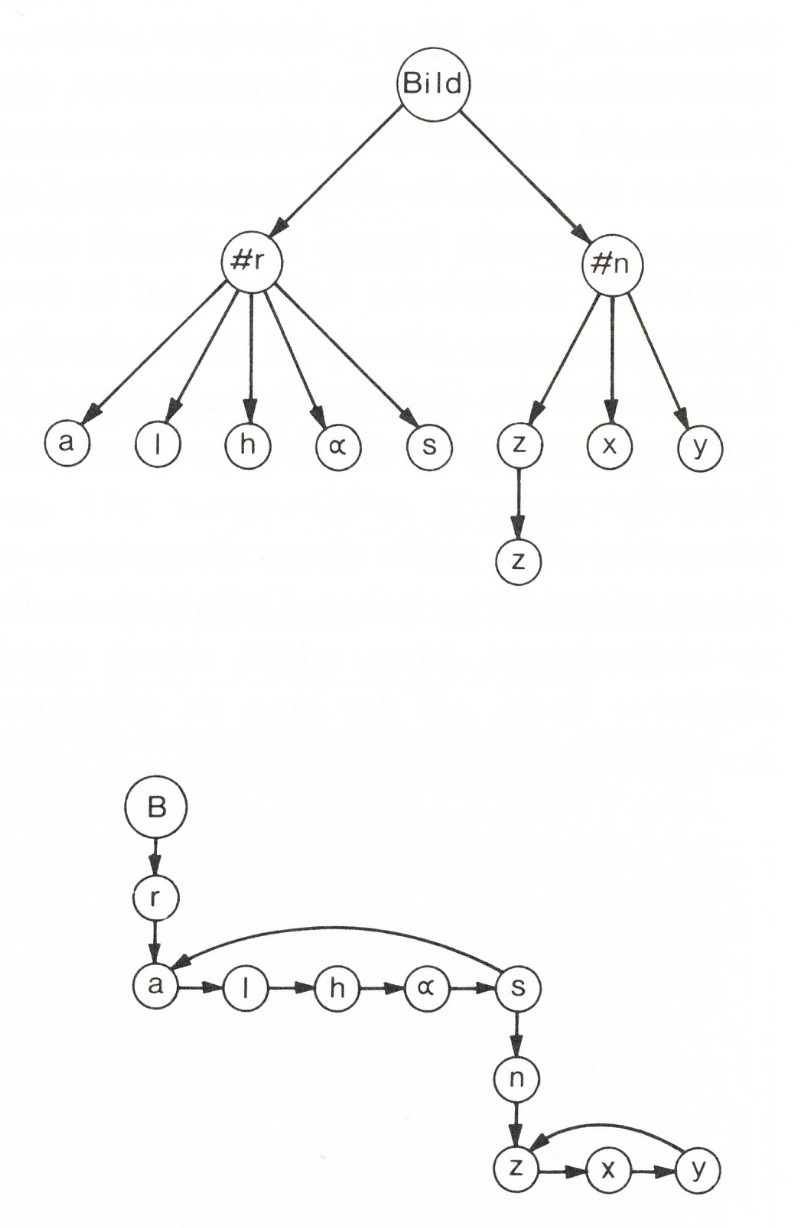
Nake, Frieder: Walk-Through-Raster, 1966, Schematische Darstellung der Baumstruktur (Nake: Ästhetik 1974, S.235, Abb. 5.5-4).

Das Programm wählte Zeichen aus einem Repertoire in Abhängigkeit "vom zuletzt gewählten Zeichen". Nach Nake simulierte das Programm ein "kurzes Gedächtnis". 42 An bestimmten Stellen wurden Zeichen gewechselt. Der Wechsel wird von programmierten "Übergangswahrscheinlichkeiten" bestimmt. 43 Ein in Rechtecke unterteiltes Feld schritt das Programm in einem von "sechs Modi" 44 ab und traf die Entscheidungen, wo welcher Übergang stattfand. Die Entscheidungswege lassen sich als Baumstrukturen darstellen, die sich sowohl in der Horizontalen als auch in der "Tiefe" 45 auffächern.

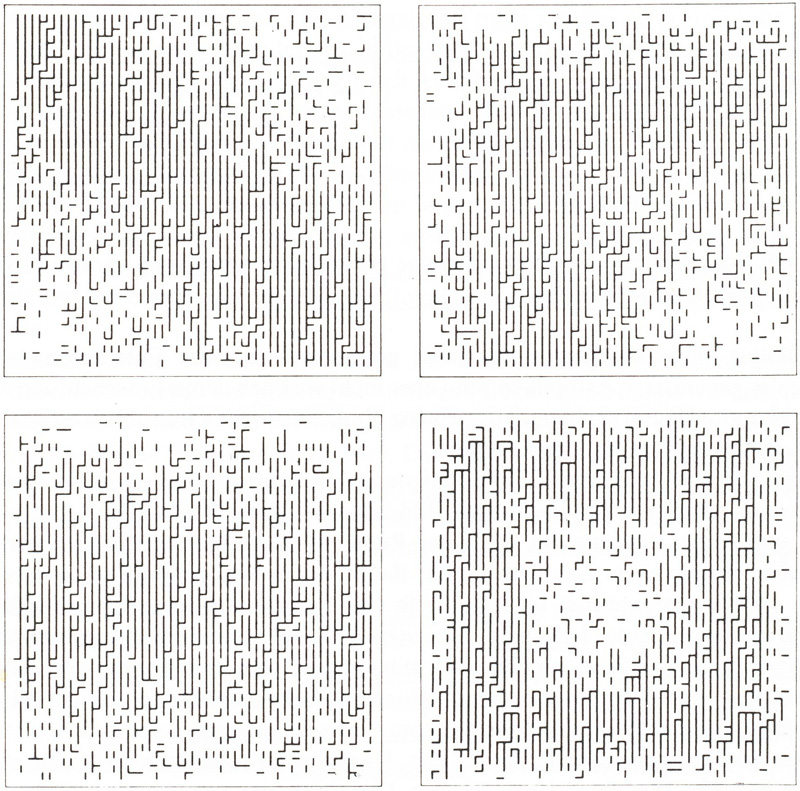
Nake, Frieder: Walk-Through-Raster, Serie 2.1, Vier Realisationen, 1966, Plotterzeichnungen (Nake: Ästhetik 1974, S.236, Abb. 5.5-5).

In der Serie "2.1" besteht das Zeichenrepertoire aus vertikalen und horizontalen Strichen sowie aus einem leeren Feld. Für die "6 Modi" der Richtungen, in denen die Schritte des Rechenprozesses über die Fläche laufen, wurden sechs Varianten mit "festem Repertoire und festen Wahrscheinlichkeiten" produziert. 46 In der Serie "7.3" wurden verschieden farbig umrissene Quadrate als Zeichen gewählt, die "bedeutend größer waren als die Rasterfelder". Die Überschneidungen der Quadrate bilden Konfigurationen, die Nake als "Zerstörung des Elementarrepertoires" beschreibt 47, nicht ohne auf Nees´ Erörterung der "Zerstörung der Matrizenanordnung" 48 zu verweisen.

Nake, Frieder: Walk-Through-Raster, Serie 7.3, 1966, vierfarbige Plotterzeichnung (Nake: Ästhetik 1974, S.237, Abb. 5.5-6).

Das "walk-through-raster"-Programm konnte "für jedes Bild einer Serie eine Anzahl informationsäthetischer Messungen" wie "Redundanz und Informationsgehalt sowie Auffälligkeit und Überraschungsmaß jedes Zeichens" 49 ausführen. Um diese Messungen als "Selektor" des Generierten in den Rechenprozess integrieren zu können, installierte Nake in seinem Programm "Generative Aesthetics I" bereits in dem "Vorselektor" statistische Maße für die Häufigkeit von Farben. Bilder mit gleicher Häufigkeit der Farben waren für den "statistischen Vorselektor" nicht unterscheidbar. 50 Die Programmierung der Verteilung in der Fläche durch den "topologischen Selektor" nach dem Maßstab von Häufigkeiten basiert auf dem Rasterprinzip:

Gegeben sei eine Wahrscheinlichkeitsverteilung p=(p₁,..., p_r) für die r Farben des Bildes. Es kommt darauf an, diese auf die Teile des Bildes zu verteilen. Dazu wird das Bild in 4 gleiche Rechtecke aufgeteilt, und die gesamte "Masse" jeder Farbe auf diese 4 Rechtecke verteilt. Für jedes der Rechtecke wird der Prozeß wiederholt usw., bis zu einem tiefsten "Niveau", das selbstverständlich nicht tiefer als die Rasterfelder selbst sein kann, in aller Regel aber schon vorher erreicht wird. 51

Der "Generator" kombiniert statistische und topologische Vorselektion in Prozeduren, die nach dem Muster von Markow-Ketten aufeinander folgen. Ein Zeilendrucker erstellt eine Notation. Deren Zeichen liefern die Informationen, wie kleine rechteckige Blättchen in vier Farben anzuordnen sind. 1969 wurden zwei Beispiele auf Hartfaserplatten realisiert. 52

Nake, Frieder: Generative Aesthetics I, 1969. Links: Experiment 6.22, Farbplättchen auf Hartfaserplatte. Rechts: Ausdruck des Ergebnisses eines Programmablaufs, Experiment 4.5a (Nake: Vergnügen 2004, o.P.).

Nake hat in "Generative Aesthetics I" eine vorher in der Computergrafik nicht erreichte Integration von Häufigkeitskriterien in den Rechenprozess realisiert. Er zeigt in dem 1974 publizierten Buch "Ästhetik der Informationsverarbeitung" Wege auf, Relationen zwischen der Vorselektion und einer Selektion nach informationstheoretischen Kriterien des "ästhetischen Maßes" zu erforschen:

Denn wie der Physiker seine Aussagen über die Natur von kontrollierten Modellen im Labor gewinnt und nachprüft, so kann man sich den Ästhetiker vorstellen, der seine Aussagen über `Kunst´ an kontrollierten Modellen seines (noch zu errichtenden) Labors gewinnt und nachprüft. 53

Nake will Benses "Generativer Ästhetik" 54, welche die Eigenschaften bereits realisierter Werke untersucht, eine Programmierung entgegensetzen, für die "ästhetische Beschreibung vor ästhetischer Wirklichkeit [als Erfahrung eines ausgeführten Werkes] möglich ist." 55

Die Informationsästhetik lieferte Anregungen für Strategien, Programmierung als Voraussetzung für die Kunstproduktion zu erproben. Die Frage nach dem "ästhetischen Maß" bleibt aktuell: Sie wird auch in aktueller Generativer Kunst im Rekurs auf kybernetische Relationen zwischen Information und Redundanz sowie Chaos und Ordnung wieder gestellt, wie Philip Galanter 2003 in "What is Generative Art? Complexity Theory as a Context for Art Theory" zeigt. 56

Dr. Thomas Dreher
Schwanthalerstr. 158
D-80339 München.
Homepage mit zahlreichen kunstkritischen Texte, u.a. zur Konzeptuellen Kunst und Intermedia Art.

Copyright © (as defined in Creative Commons Attribution-NoDerivs-NonCommercial 1.0) by the author, November 2011/August 2015.
This work may be copied in noncommercial contexts if proper credit is given to the author and IASL online.
For other permission, please contact IASL online.

Wollen Sie dazu Stellung nehmen oder einen eigenen Tip geben? Dann schicken Sie uns eine E-Mail.

Anmerkungen

1 Laposky: Oscillons 1953, S.2. zurück

2 Laposky: Oscillons 1976. zurück

3 Franke/Nierhoff-Wielk: Ästhetik 2007, S.110 (Zitat); Herzogenrath/Nierhoff-Wielk: Machina 2007, S.336,338, Nr.68f.; Piehler: Anfänge 2002, S.149-152, o.P. mit Abb.29f . zurück

4 Herbert W. Franke, e-Mail, 17.8.2015. Franke schreibt dort über die "die übliche Einstellung eines Oszillographen": "Bei dieser bewegt sich der Elektronenstrahl auf der Grundlinie hin und her, wobei er langsam (mit dem Auge verfolgbar) von links nach rechts läuft und sprunghaft wieder zurück. Dabei würde am unteren Bildrand eine waagrechte gerade Linie entstehen. Diese wird aber durch die in y-Richtung weisenden Impulse des Messvorgangs verformt, so dass ein 'Abbild' des Wechselstrom-Verlaufs entsteht. Verändert man probeweise die Einstellungen, dann ergeben sich 'sinnlose' andere Bildergebnisse...Den Analogrechner brauchte ich, um eine Kurve z(x,y) zu erzeugen. Der Wert z steht für die Helligkeit des Bildes auf dem Bilddschirm. x und y sind die Koordinaten [der Horizontal- und Vertikalachsen] des Lichtspuren auf dem Bildschirm hinterlassenden Bildpunkts. Die Kurve kommt folgendermaßen zustande: Der Analogrechner erzeugte zwei Funktionen f1x(t) und f2y(t) in Abhängigkeit der Zeit t, physikalisch als zwei voneinander unabhängige Schwingungen (von deren Frequenz die Formen abhängen und die sich in Echtzeit einstellen und verändern lassen)." zurück

5 Herzogenrath/Nierhoff-Wielk: Machina 2007, S.150,232,362f., Nr.150f.; Nierhoff-Wielk: Machina 2007, S.28f. zurück

6 o.T., 1960, Plotterzeichnung. In: Alsleben: Redundanz 1962, S.52. mit Abb. d; Piehler: Anfänge 2000, S.204f., o.P. mit Abb.33; Rosen: Story 2008/2011, S.248.
Über die Plotterzeichnungen von Alsleben und Passow: Alsleben: Redundanz 1962, S.51f.; Alsleben/Eske/Idensen: Aestheticus 2011, S.149ff.; Herzogenrath/Nierhoff-Wielk: Machina 2007, S.65,234,297f.; Nierhoff-Wielk: Machina 2007. S.27f.; Piehler: Anfänge 2000, S.203ff., o.P. mit Abb. 33f.; Reichhardt: Serendipity 1968, S.94; Weiß: Netzkunst 2009, S.326ff. zurück

7 IBM lieferte den ersten FORTRAN-Compiler ab April 1957 aus (o.A.: User Notes 1996-98). Der Electrologica X1 Compiler (August 1960) von Edsger Wybe Dijkstra und Jaap A. Zonneveld gilt als der erste Compiler für ALGOL60 (Daylight: Dijkstra 2010).
Über Plotter: Piehler: Anfänge 2000, S.177-180. zurück

8 In Gerhard Stickels "Autopoemen" von 1965 werden auch die syntaktischen Strukturen von einem Zufallsgenerator gewählt (s. Kap. III.1.3), doch ist die Häufigkeit des Zugriffs auf einzelne Strukturen – im Unterschied zu Lutzs "stochastischen Texten" – nicht beschränkt. zurück

9 Bense: Aesthetica 1982, S.33f.,322f.,328f.,354f.; Bense: Einführung 1965/1968, S.30-35; Bense: Einführung 1969, S.43ff.,55f.; Bense: Informationstheorie 1963/2000, S.136; Birkhoff: Measure 1933. zurück

10 Moles: Information 1965/1968, S.23; Moles: Kunst 1973, S.20ff. zurück

11 Bense: Aesthetica 1982, S.212,325; Bense: Einführung 1965/1968, S.34; Shannon: Communication 1949, S.16. zurück

12 Über das "ästhetische Maß" bei Birkhoff, Bense, Moles und anderen: Nake: Ästhetik 1974, S.75ff,82ff. zurück

13 Bense: Aesthetica 1982, S.147,211,214f.,217,223,225 (Zitat). zurück

14 Moles: Informationstheorie 1971, S.220,243f. zurück

15 Cage bezeichnet seine Zufallsverfahren als nicht determiniert (Schulze: Spiel 2000, S.161-179), während die Informationsästhetik von der Stochastik (s. Kap. II.1.2) ausgeht: Die Wahrscheinlichkeit, dass ein Element per Zufallsverfahren ausgewählt wird, ist bereits durch die Auswahl der Elemente und der Kombinationsmöglichkeiten determiniert. Florian Cramer weist Cage nach, dass auch seine Zufallsverfahren der Determinierung nicht entrinnen können (Cramer: Statements 2011, S.199-202). zurück

16 Götz: Malerei 1961, S.14 mit Fig.1, S.23 (Zitate). Vgl. Götz: Erinnerungen 1983, S.899f.,902; Klütsch: Computergrafik 2007, S.148; Mehring: Television Art 2008, S.36.
Weitere Beispiele "Statistisch-Metrischer Modulationen" in: Beckstette: Bildstörung 2009; Götz: Erinnerungen 1983, S.869-905; Kersting: Sammlung Etzold 1986, S.206 (mit vier Beispielen, die im Sommer 1959 entworfen und im Februar 1960 ausgeführt wurden).
Vorläufer der aleatorischen Anordnung von Quadraten: Kelly, Ellsworth: Spectrum Colors Arranged by Chance I-VIII, 1951, Collagen aus farbigen Papieren. In: Bois/Cowart/Pacquement: Kelly 1992, S.42ff.,168ff.,192. Morellet, François: Repartitions aléatoires, ab 1958, Öl oder Acryl auf Leinwand. In: Holeczek/Mengden: Zufall 1992, S.23,46f.,278-281. zurück

17 Julesz: Dialoge 1997, S.137. zurück

18 Kovács: Julesz 2007. zurück

19 Julesz: Depth Perception 1960, S.1127,1134. zurück

20 Julesz: Depth Perception 1960, S.1134f.; Noll: Beginnings 1994, S.39. zurück

21 Julesz: Depth Perception 1960, S.1128 mit Fig.2, S.1154,1159. zurück

22 Julesz: Depth Perception 1960, S.1128 mit Fig.3, S.1156,1159. zurück

23 Julesz: Foundations 1971; Kovács: Julesz 1997; Weibel: Konturen 1997, S.40f.
1979 entwickelte Christopher W. Tyler "Autostereogramme". Die Tiefenwirkung der "Random Dot Stereograms" wird in den "Autostereogrammen" durch ein Einzelbild provoziert (Tyler/Clarke: Autostereogram 1990). zurück

24 Julesz: Dialoge 1997, S.138. zurück

25 Noll: Beginnings 1994, S.39. zurück

26 Noll: Patterns 1962, S.4. zurück

27 Herzogenrath/Nierhoff-Wielk: Machina 2007, S.445 (Zitat); Klütsch: Computergrafik 2007, S.166f.; Noll: Human 1966, S.2. zurück

28 Noll: Patterns 1962, S.2f. zurück

29 Noll: Computers 1967, S.67. zurück

30 Davis: Experiment 1975, S.120; Herzogenrath/Nierhoff-Wielk: Machina 2007, S.444ff., Nr.356; Klütsch: Computergrafik 2007, S.167ff.; Noll: Computers 1967, S.67; Piehler: Anfänge 2000, S.235f., o.P. mit Abb.46; Reichardt: Serendipity 1968, S.74; Rosen: Story 2008/2011, S.249.
Auch wenn Noll sich nicht von der Informationsästhetik anregen ließ (Klütsch: Computergrafk 2007, S.165f.), so liefert er mit seinen Werken doch Modelle für Fragen nach dem "ästhetischen Maß". zurück

31 Nake: Ästhetik 1974, S.199. zurück

32 Nees: Variationen 1964. Vgl. Nees: Computergraphik 1969/2006, S.XIf., Abb.4; Nees: Künstliche Kunst 2005, o.P. mit Abb.1f. zurück

33 Nees: Computergraphik 1969/2006, S.208. zurück

34 Nees: Computergraphik 1969/2006, S.208. zurück

35 Beispiele in: Herzogenrath/Nierhoff-Wielk: Machina 2007, S.434f., Nr. 309f.; 314, 317ff.; Nees: Computergraphik 1969/2006, S.216ff. und 222ff. mit Bild 28-33, S.231 mit Bild 36, S.244 und 247f. mit Bild 39-41. zurück

36 Nees: Computergraphik 1969/2006, S.27: "Die Perzeptionsabhängigkeit des Bildnexus..." zurück

37 Nees: Computergraphik 1969/2006, S.29. Auf S.24 zitiert Nees Max Benses 1965 in Teil V der "Aesthetica" publizierte Unterscheidung von "Mikro-" ("Ordnungen und Komplexität") und "Makroästhetik" ("Redundanzen und Information") ausführlicher (Bense: Aesthetica 1982, S.334. Vgl. Klütsch: Computergrafik 2007, S.67-71). zurück

38 Nees: Computergraphik 1969/2006, S.209. zurück

39 Nees: Computergraphik 1969/2006, S.220. zurück

40 Nees: Computergraphik 1969/2006, S.213. Vgl. S.177 mit einem weiteren Zitat aus Max Benses Ästhetik (Teil V von 1956. Neu in: Bense: Aesthetica 1982, S.142) über hier relevante Kriterien der Unterscheidung von "Mikro-" und "Makroästhetik" (s. Anm.37). zurück

41 Nake, Frieder: Zufälliger Polygonzug, Plotterzeichnung, 1963/64: Herzogenrath/Nierhoff-Wielk: Machina 2007, S.424, Nr.259 (Sammlung Herbert W. Franke); Klütsch: Computergrafik 2007, S.131-139; Nake: Ästhetik 1974, S.199f. mit Abb. 5.2-7. Nake bildet denselben "Zufälligen Polygonzug" mit dem Entstehungsdatum 1963 und der Größenangabe 10 x 10 cm ab, der sich auch in der Sammlung Franke (Kunsthalle Bremen) befindet und der "6/7/64" (7. Juni 1964) mit dem Programm COMPART ER 56 und einem Zuse Graphomat Z64 erstellt worden sein soll (Maße 15,5 x 11,5 cm auf einem Blatt mit der Größe 21,1 x 15,1 cm). Das Programm COMPART ER 56 ist nach Nake: Ästhetik 1974, S.192 und Klütsch: Computergrafik 2007, S.132 ab 1964 entwickelt worden, nach Herzogenrath/Nierhoff-Wielk: Machina 2007, S.236 jedoch bereits ab 1963.
Weitere frühe digitale Computergrafiken: Electronic Associates Incorporated (EAI): Stained Glass Window, 1963 (Herzogenrath/Nierhoff-Wielk: Machina 2007, S.63,238 mit Abb.13, S.332, Nr.66); Bäumer, Wolfgang: ohne Titel, 1963/64 (Herzogenrath/Nierhoff-Wielk: Machina 2007, S.94,309, Nr.9f.); Kawano, Hiroshi: Design 2-1 Markov Chain Pattern, 1964 (Rosen: Kawano 2011); Sumner, Lloyd: Eye´s Delight, 1964 (Dika: Computerkunst 2007, S.75ff., Abb.32). zurück

42 Nake: Ästhetik 1974, S.229. zurück

43 Nake: Ästhetik 1974, S.232. zurück

44 Nake: Ästhetik 1974, S.229. zurück

45 Nake: Ästhetik 1974, S.235. zurück

46 Herzogenrath/Nierhoff-Wielk: Machina 2007, S.426, Nr.267; Klütsch: Computergrafik 2007, S.152ff.; Nake: Ästhetik 1974, S.236f. mit Abb.5.5-5; Rödiger: Algorithmik 2003, S.98,134,141,164. zurück

47 Herzogenrath/Nierhoff-Wielk: Machina 2007, S.426f., Nr.268,271,273; Nake: Ästhetik 1974, S.237f. mit Abb. 5.5-6. zurück

48 Nake: Ästhetik 1974, S.241; Nees: Computergrafik 1969/2006, S.208f. zurück

49 Nake: Ästhetik 1974, S.236,262. zurück

50 Nake: Ästhetik 1974, S.263. Nake hat "Generative Aesthetics I" zum ersten Mal 1970 auf dem Symposium "Computer Graphics 70" in Uxbridge vorgestellt (Nake: Generative Aesthetics 1970). zurück

51 Nake: Ästhetik 1974, S.264-271. zurück

52 Nake: Ästhetik 1974, S.273-276 mit Abb.5.8-7, 5.8-8 (Beispiele für Notation und Farbblättchen von 1969). Die Vorselektoren "wurden 1969 an der University of Toronto für eine IBM 360-65 [ab November 1965] in PL/I implementiert" (ebda, S.273). Nake: Brief 1973, S.225: "Realisiert wurden allerdings nur zwei Exemplare – und das von Hand, weil ich gerne größere Formate als mit den mir damals zugänglichen Zeichenmaschinen erreichbar produzieren wollte." Vgl. Klütsch: Computergrafik 2007, S.155-158 mit Abb. 33ff. zurück

53 Nake: Ästhetik 1974, S.277. zurück

54 Bense: Aesthetica 1982, S.333-338. zurück

55 Nake: Ästhetik 1974, S.277. zurück

56 Galanter: Generative Art 2003 mit Bezug auf Moles: Informationstheorie 1973. zurück